The autumn equinox - well, autumn in the northern hemisphere - came and went a few weeks ago. I spent it, as I mentioned in my last column here, at the Hanle Dark Sky Reserve in north India. Four nights with some 40 other amateur astronomers, in the open at 14,000 feet, temperatures hovering just below freezing, photographing the splendid night sky.

But on that equinox in particular, I was a fascinated spectator as a young PhD student in Physics from the Indian Institute of Science Education and Research (IISER) Pune, Sourabh, channeled his inner Eratosthenes. Maybe mine too.

That's Eratosthenes the ancient Greek mathematician. But he was many other things too - a historian, an astronomer, a librarian, a musician and, perhaps most relevant to Sourabh on equinox day in Hanle, a geographer. To read about him is to think, this was a Renaissance Man before we knew the term. And at our homestay in Hanle, Sourabh set out to replicate this ancient Renaissance Man's most famous experiment.

Which is ... well, let's see how Sourabh went about it.

September 22, the equinox: a bright, sunny day in Hanle. Shirtsleeve temperatures by mid-morning even though it had been near zero at night. Cloudless brilliant blue sky augurs well for more stargazing tonight, our last night here. But right now the sun dazzles, casting sharp shadows.

In one corner of the homestay's yard is a pole stuck in the ground, about 3 feet tall. When we walk over, it is actually a length of grey PVC pipe and it isn't clear why it stands here. Unless ... maybe it's meant for Eratosthenes-style experiments? It certainly fits the bill. It casts a shadow and it makes a near-right angle with the ground. In fact, the ground right around it is a small expanse of flat concrete, which will shortly prove its convenience.

But Sourabh doesn't want to rely solely on this pole. He has also opened his notebook flat on a small table. Using a lump of clay, he has erected a pencil there, also forming a near-right angle with the book. He carefully positions the contraption so the pencil casts a distinct shadow across the whiteness of the page. He sets up his phone on a tripod to film the whole exercise. Friend Rashmi, herself an accomplished science communicator who goes by "astro_roxy" on Insta, is every bit as excited about the experiment. She joins in, live-streaming the proceedings and explaining what's happening to her nearly 50,000 followers.

About ten minutes before noon - understood as solar noon, the moment the sun reaches its zenith, which is not necessarily 12 noon - Sourabh is ready to start. What he and Rashmi want to do is measure the length of the shadows - pole and pencil both - at this solar noon. But how do they know exactly when that moment is? There are websites that will give you the precise time for your precise location. But Eratosthenes didn't have helpful websites, so why should Rashmi and Sourabh use one today? Instead, he used what we know about the sun at its zenith: that's when the shadows it casts are shortest.

So: about every half-minute or so, over at the PVC pole, Rashmi places a pebble at the tip of the shadow it casts on its cement surrounds. Similarly, Sourabh marks a red dot at the tip of the shadow his pencil casts on his notebook. They do this over about 20 minutes. In theory, this should leave stones and dots forming gentle curves. That's because of the sun's apparent motion across the sky, and because the shadows steadily shorten till solar noon, and then start lengthening again. And if you have that gentle curve, it should be possible to spot the pebble, or the red dot, that's closest to the pole, or pencil.

In practice, the curves are so gentle that they are practically straight. Still, Rashmi points to the pebble she thinks marks the shortest pole shadow. Sourabh picks the dot that marks the shortest pencil shadow. They measure and note down those lengths. They have earlier measured and noted the lengths of pole and pencil. What they are after is the angle formed by the sun's rays at its zenith, and the pole (pencil) itself. If you remember your trigonometry, the ratio between shadow length and pole (pencil) length is the tangent of that angle. So if we calculate that ratio, we know the angle.

Why solar noon, though, and why the equinox? Both are really just conveniences. On the equinox, we know that the sun is directly above the equator. So, at noon on that day, a pole on the equator will not have a shadow. We could also do this on either of the solstices, when we know that the sun is above the Tropic of Cancer (summer solstice) or the Tropic of Capricorn (winter solstice), and will, at solar noon, cast no shadows there. In contrast, at that same moment in Hanle, the pole casts a shadow, and we can calculate the angle that pole makes with the rays of the sun.

And why are we interested in that angle? Well, to begin with, it was what told Eratosthenes a fundamental truth about the planet he inhabited. Where he lived in Alexandria, a pole cast a shadow at noon on the summer solstice. But at the same time in distant Syene (today's Aswan), almost exactly on the Tropic of Cancer, the sun was directly over a well he knew about - and no shadow there. Now if the Earth was flat, as many of Eratosthenes' contemporaries believed, at any given moment the sun would make the same angle with any given pole anywhere on the planet. But this observed difference between Syene and Alexandria meant the Earth had to be ... curved. Like a ball.

But there was more to that angle. If you project the pole at Alexandria and the well at Syene down into the Earth, those two lines will meet at the centre of the planet, forming an angle. The Sun is so far from us that its rays are effectively parallel when they reach us. Simple geometry about parallel lines tells us that that angle is the same as the angle formed by the pole in Alexandria - the two are known as alternate interior angles. So here's what Eratosthenes reasoned: if that angle corresponds to the distance between Syene and Alexandria, then 360 degrees corresponds to the circumference of the Earth.

Such a simple thought - and yet I can almost sense how much it meant to Eratosthenes. For here he was, about to find out just how large his world - our world - really is. He paid someone to travel between Syene and Alexandria and report the distance between the two cities. He multiplied that by 360 and divided by the angle his pole made. The answer: nearly 40,000 km, astonishingly close to the generally accepted modern figure of 40,075 km at the equator.

And in Hanle on autumn equinox 2025, this is what Rashmi and Sourabh were chasing. Note that unlike Eratosthenes, they didn't need to pay anyone to pace out the distance between the Equator and Hanle. That's easily calculated. One degree of latitude is about 111km, and you can look up Hanle's latitude: 32.78N. Multiply those two and we know Hanle is about 3640 km from the Equator. So if Rashmi and Sourabh's measured angles correspond to 3640 km, then 360 degrees must correspond to ...

Well, hold that thought. But also ask this question: given the angle they measured, did they need to look up Hanle's latitude at all?

Actually, we could really do this experiment on any (sunny) day of the year. After all, what we are interested in is the difference in the angles between pole and the sun's rays, as measured at solar noon at two different spots on the Earth. On the equinoxes or solstices, we know already that that angle is zero at specific latitudes (0, 23.5S, 23.5N). This makes calculating the angle difference easy. Just as easy is the calculation of the distance between where you are and the relevant line of latitude.

But at noon on any other day of the year, that angle is also zero somewhere on the planet between the two Tropics, and there are websites and apps that track this. Another Hanle colleague, Alok Mandavgane, has this one. It tells me, for example, that 15 May next year is such a day in Bombay. As long as you know how far it is from Bombay to Hanle, or wherever on Earth you are then, you can do the Eratosthenes thing on that day too.

Actually, you could do it at any time on any (sunny) day, without caring about zero shadows or waiting for solar noon. Since what we are interested in is the difference between the angles, we just need to measure them at the same moment on both days, and subtract one from the other. Admittedly this simultaneous measurement is harder to pull off than if we can conveniently assume one of those angles is zero. But it's the principle, of course.

So what did Rashmi and Sourabh find? Using the pencil and its shadow, they calculated the planet's circumference as 40,852 km. Using the pole in the yard, they got 39,483 km.

Compare those numbers to 40,075 km, the Earth's girth at the equator, and join me in applauding Rashmi and Sourabh.

Yet as close as they came with their calculation, to me the point of their exercise on that equinox day wasn't about getting close. Instead, it was about thinking of what a great mind did 2200 years ago, of its significance, and then finding ways to duplicate his effort. A pencil and a pole, their tools to better understand our world.

And in doing so, to feel the wonder and awe that Eratosthenes must have felt.

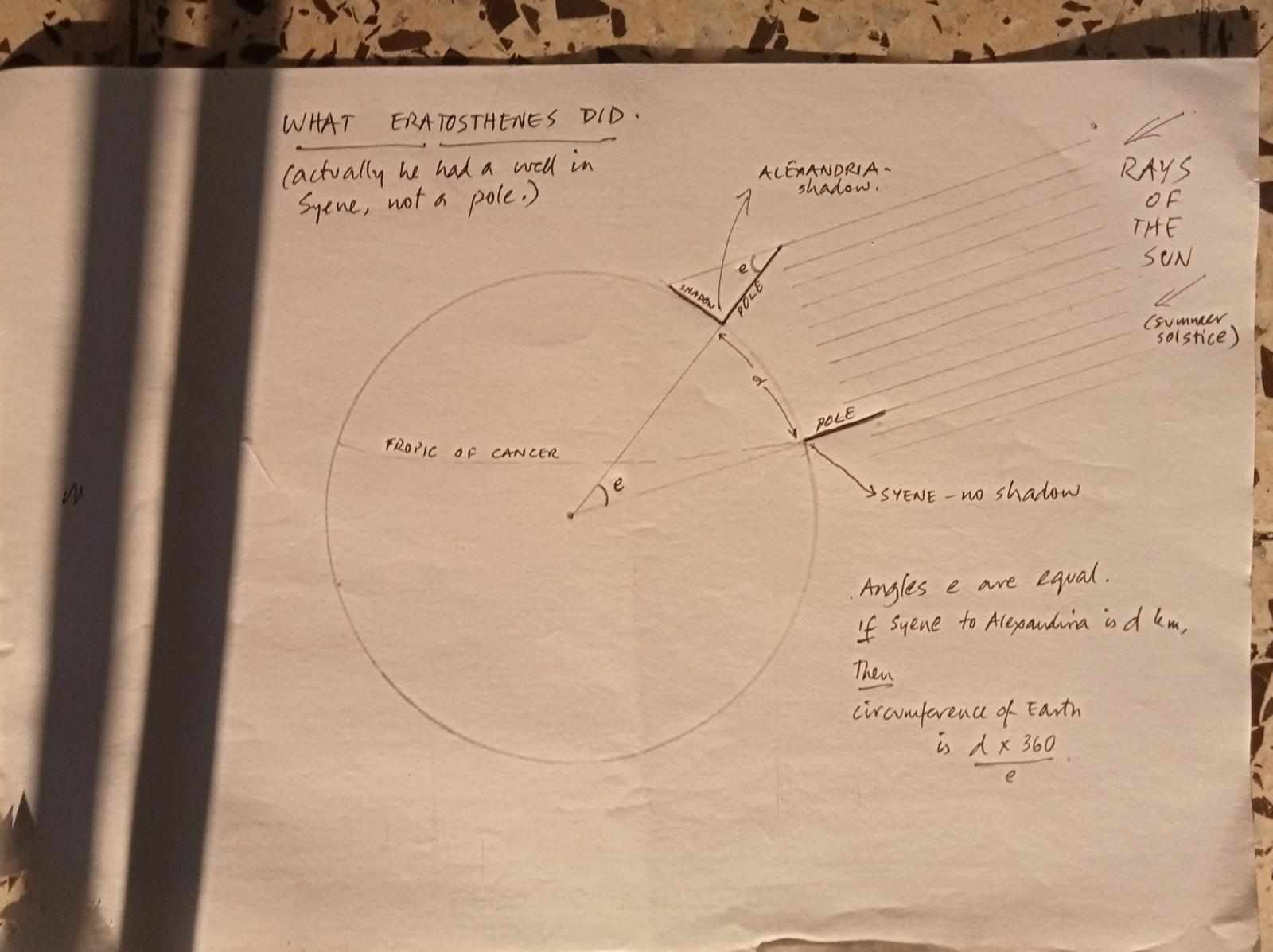
PS: No, they didn't need to look up Hanle's latitude. A little thought will tell you that the angle between Sourabh's upright pencil and the sun's rays is the latitude of that spot.

PS #2: Music reference somewhere above: kudos if you can tell me what.

(This article originally appeared on 3 Quarks Daily here.)

Hanle Dark Sky Reserve (HDSR) is a joint initiative of the Union Territory of Ladakh Administration, the Indian Institute of Astrophysics (IIA), Ladakh Autonomous Hill Development Council (LAHDC) Leh, and local communities.